Distributed Ledger Technologies
The so-called blockchain has a relatively short history, being only introduced as early as 2008 by someone (or someones) going under the pseudonym Satoshi Nakamoto. A blockchain is an append-only database where each new update to the database refers to the previous state of the database. Each previous state contains the updates and a hash of the updated database (and other information) and is known as a block. Diagramatically, the blocks appear in a chain, hence the name.
In his seminal paper on Bitcoin, Nakamoto introduces a new form of consensus, now commonly referred to as Nakamoto consensus, where the rule is that the longest chain is the correct chain. Nakamoto was able to create a permissionless database (permissionless in the sense anyone could freely join or leave, amongst other things) by incentivizing participants with an economic reward. Due to this game theoretic incentivization, Nakamoto argued that honest participants would only work on the correct chain (almost by definition).
Nakamoto consensus (although not practically) can withstand a higher percentage of adversaries (up to 50%) compared to traditional Byzantine Fault Tolerant (BFT) consensus models (up to 1/3 faulty nodes / malicious actors). Theoretically, Nakamoto consensus is strictly probabilistic as it does not have the same finality of the state as BFT models do.
High Performance Computing
This work involves optimizing computer code to decrease cache misses, decrease data movement from host (CPU server) to the device (GPU), develop and analyze algorithms for particular scientific domains, and refactoring data structures. Using OpenMP4.5 or OpenACC pragma directives allows for easily porting code between a CPU-only parallel supercomputer and supercomputers that have GPUs. However, portable code that can run on both architectures fairly well takes a slight performance hit in that neither hits the theoretical peak.
Nonlinear Polynomial Root Finding
Finding all the isolated solutions of a system of polynomial equations is a common problem that appears throughout all the sciences. This has been an active area of interest in mathematics and has historical origins dating back to Babylonian times. The foundations for numerical algebraic geometry began with classical algebraic geometry in the 18th and 19th centuries. In the early 20th century, continuation methods were widely used for solving perturbed differential equations. Not until the late 1970's were the necessary pieces put together to begin the emergence of the field numerical algebraic geometry.
Numerical algebraic geometry aims at discovering effective numerical or hybrid symbolic-numeric algorithms that can find all the isolated solutions and has been an active area of research for nearly four decades. Applications are numerous and an incomplete list includes: biochemical reaction networks, string theory, rock magnetism, geometric complexity theory, robotics, differential equations, and optimization.
Let us review some mathematical background, starting with varieties and ideals. I will keep it as simplified as possible. OK. Here we go . . .
Algebraic varieties are a basic object of study in algebraic geometry. These varieties are generated by ideals, i.e. equations over some polynomial ring. I normally let $$R = \mathbb{C}[x_1, \dots, x_n],$$ but you can pick your favorite ring.
The varieties are then the set of common zeroes of these equations. These varieties can be 0-dimensional, i.e. isolated solutions, or positive-dimensional, i.e. an infinite number of (complex) solutions. Thanks to a classical algebraic geometry theorem due to Bertini in conjunction with Bèzout's Theorem, we can study the positive dimensional case by restricting ourselves to an appropriate 0-dimensional variety.
A standard tool in numerical algebraic geometry is homotopy continuation. Essentially, if you give me a polynomial system, say $f(z)$, then I can construct a suitable system $g(z)$ and a homotopy $H(z; t)$ such that for every isolated solution $z^*$ of $f(z)$, there exists a homotopy path between $z^*$ and one solution of $g(z)$.
Given a proper $g(z)$, one suitable homotopy is $$H(z; t) = \gamma g(z)t + (1 - t)f(z),$$ where $\gamma \in \mathbb{C}$ and $t$ varies from $1 \to 0$. Note that $H(z; 0) = f(z)$ and $H(z; 1) = \gamma g(z)$. The generic $\gamma$ is used because this homotopy will now avoid a set of `bad' points with probability $1$. The generic $\gamma$ allows one to use the underlying algebraic geometry of the complex numbers, even when all the coefficients of $f$ or $g$ are real. For most applications, scientists are only interested in real solutions, but the solutions don't actually become real until the $t = 0$. In fact, this method will find all the complex solutions!
In a topological sense, a homotopy is the continuous transformation of one topological space into another topological space. In our situation, we are endowed with the Zariski topology. This is because the zero set of a system of equations over the complex ring of $n$ variables are the closed sets in this topology. Using predictor-corrector methods (think Euler + multivariate Newton), we homotopically deform the solutions of the start system to the solutions of the target system by slowly perturbing the underlying polynomial system.
Here's a nice picture that helps to visualize what's happening. Albeit, the picture is not entirely truthful because we are sitting in some higher dimensional space and not tracking paths in the plane, but it gives the general idea.
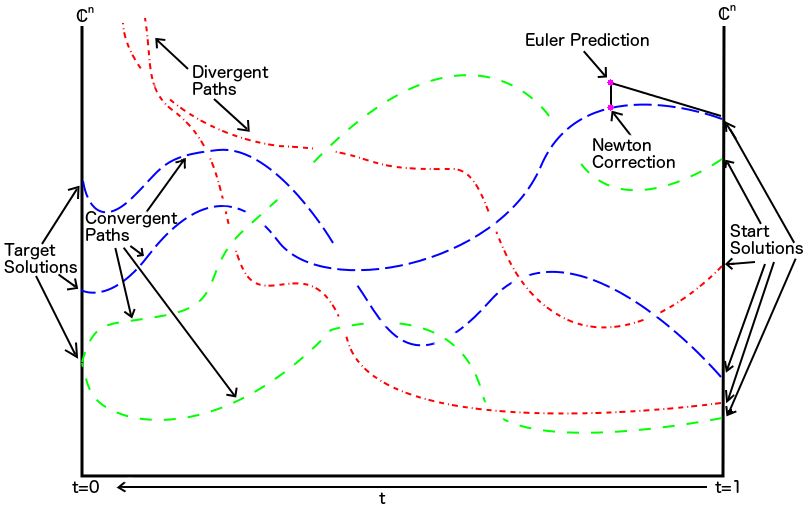
A lot more is happening behind the scenes, and properly implementing this into software is a non-trivial task.
Fortunately, several software packages have been specifically written (and under active development!) with this purpose in mind; each of the software packages available have their own flavors, but all are general-purpose dense polynomial system solvers. The latter two also have polyhedral methods incorporated, while the former in this list does not (currently). These polynomial system solvers are:
I am an active developer of the next version of Bertini, which is currently undergoing a rewrite from C to C++. I also am a co-author of several other software packages.
For a good reference on the most up-to-date results and open research problems in numerical algebraic geometry, check out the Bertini book.
Numerical algebraic geometry has a non-empty intersection with many areas of mathematics, the sciences, and engineering. A lot of opportunities exist to conduct both mathematical and interdisciplinary research.
In summary, I investigate basic questions that arise from the study of finding approximate solutions to polynomial or polynomial-like systems of equations.
I have some research projects in which I am partially supported by public funds. Any data and software created from such projects will be publicly available. If you come across a paper I have co-authored and these materials are not readily available, do not hestiate to ask me for them.
My expertise allows me the opportunity to work in many areas. I will have some more information regarding my current and past research.
In addition to numerical and computational algebraic geometry, I find machine learning, quantum computation, tropical geometry, and much more quite fascinating.
Contact me if you are interested in collaborating on a project!