Here are some images for the example I emailed about:
This is J2 (green) and J1 (magenta).

This is J2 (green) and g (blue).
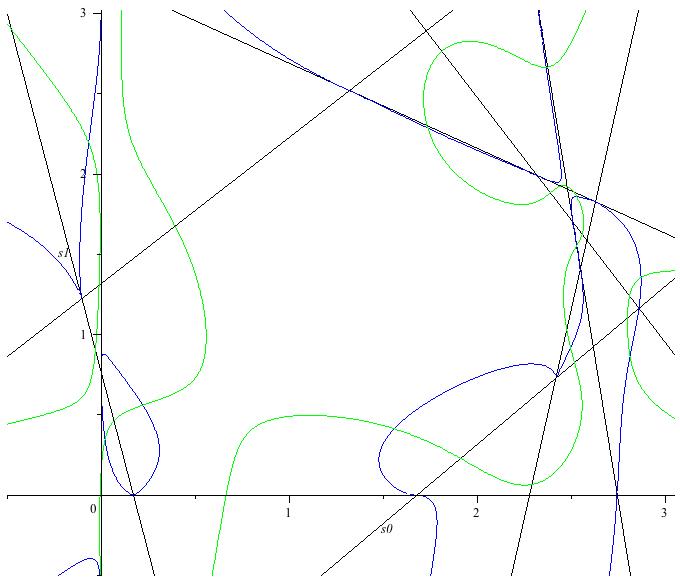
This is J2 (green) and f (red).
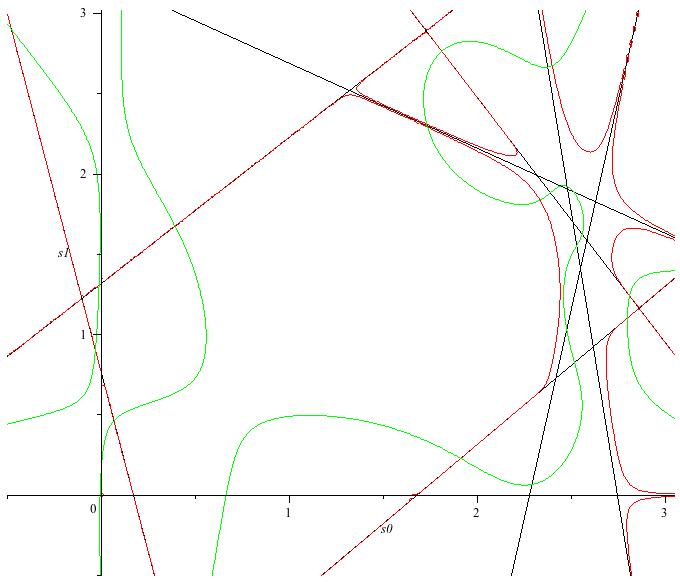
This is f (red) and g (blue).
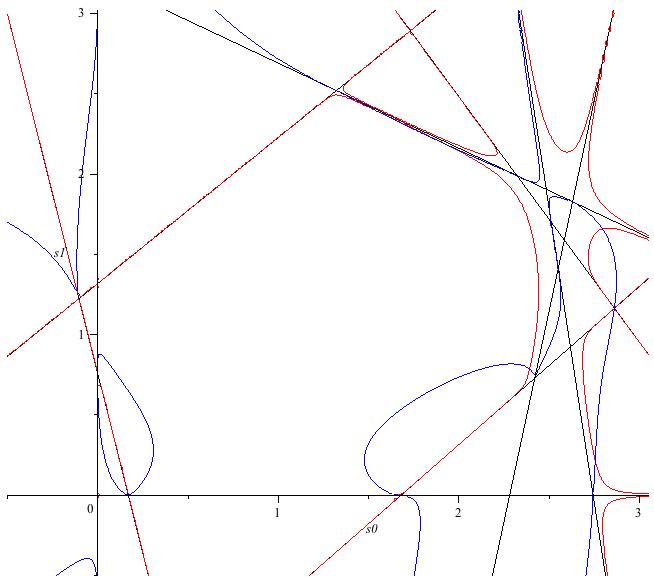
This corresponds to fewnomial system in this file. The gale system is
$f = (\frac{76}{17}s_0+s_1-\frac{19}{25})^1(-\frac{73}{74}s_0+s_1+\frac{1533}{925})^1(-\frac{68}{13}s_0+s_1+\frac{15507}{1300})^4(-\frac{29}{4}s_0-s_1+\frac{7959}{400})^5$
$\hspace{50mm}(-\frac{29}{19}s_0-s_1+\frac{10509}{1900})^1(-\frac{53}{100}s_0-s_1+\frac{8049}{2500})^4(\frac{10}{11}s_0-s_1+\frac{33}{25})^3(s_0)^1(s_1)^4
- 1$
$g = (-\frac{68}{13}s_0+s_1+\frac{15507}{1300})^4(-\frac{29}{19}s_0-s_1+\frac{10509}{1900})^5(\frac{10}{11}s_0-s_1+\frac{33}{25})^5(s_0)^1(s_1)^3$
$\hspace{50mm} - (\frac{76}{17}s_0+s_1-\frac{19}{25})^4(-\frac{73}{74}s_0+s_1+\frac{1533}{925})^5(-\frac{29}{4}s_0-s_1+\frac{7959}{400})^3(-\frac{53}{100}s_0-s_1+\frac{8049}{2500})^3$